Рост популяций и кривые роста
Если рождаемость в популяции превышает смертность, то популяция, как правило, будет расти. С увеличением плотности скорость роста популяции постепенно снижается до нуля. При нулевом росте популяция стабильна, т. е. размеры ее не меняются. Отдельные организмы при этом могут расти и размножаться. Нулевая скорость роста означает лишь то, что скорость размножения, если оно происходит, уравновешена смертностью. Данная картина характерна для ряда одноклеточных и многоклеточных организмов, например для клеток водорослей в культураль-ной жидкости, для фитопланктона озер и океанов весной, для насекомых (мучные хрущаки, а также клещи, интродуцирован-ные в новое местообитание с обильными запасами пищи, где нет хищников).
Миграция, или расселение, так же как и внезапное снижение скорости размножения, может способствовать уменьшению численности популяции. Расселение может быть связано с определенной стадией жизненного цикла, например с образованием семян. Рассматривая вопрос об оптимальных размерах популяции в данной среде, следует учитывать поддерживающую емкость или кормовую продуктивность среды. Чем выше поддерживающая емкость, тем больше максимальный размер популяции, который может существовать неопределенно долгое время в данном местообитании. Дальнейшему росту популяции будут препятствовать один или несколько лимитирующих факторов. Это зависит от доступности ресурсов для данного вида.
Таким образом, скорость роста популяции в естественных местообитаниях будет зависеть от климатических изменений, от снабжения пищей и от того, ограничено ли размножение определенным временем года и др., что должно учитываться при составлении моделей или их усовершенствовании.
Математические модели экспоненциального роста популяций и роста при ограниченных ресурсах. Рост численности популяции в геометрической прогрессии можно описать с помощью простых уравнений. Так, в популяции с исходной численностью в N особей за промежуток времени t появляется N новых особей. Если число вновь появившихся особей прямо пропорционально N и t, то имеем уравнение N = r t N. примечание: t - это дельта T, изменение времени. Разделив обе его части на t, получим
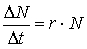
Величина 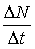 - абсолютная скорость роста численности, - абсолютная скорость роста численности,
г — биотический потенциал или удельная скорость роста численности.
За малый промежуток времени изменение численности равно ее производной
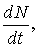 и уравнение (9.4) можно переписать так: и уравнение (9.4) можно переписать так:
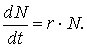 Решение этого уравнения — функция Решение этого уравнения — функция 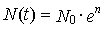
Здесь е — основание натуральных логарифмов (е 2,72...). График этой функции и есть экспонента (рис. 9.10,вверху). 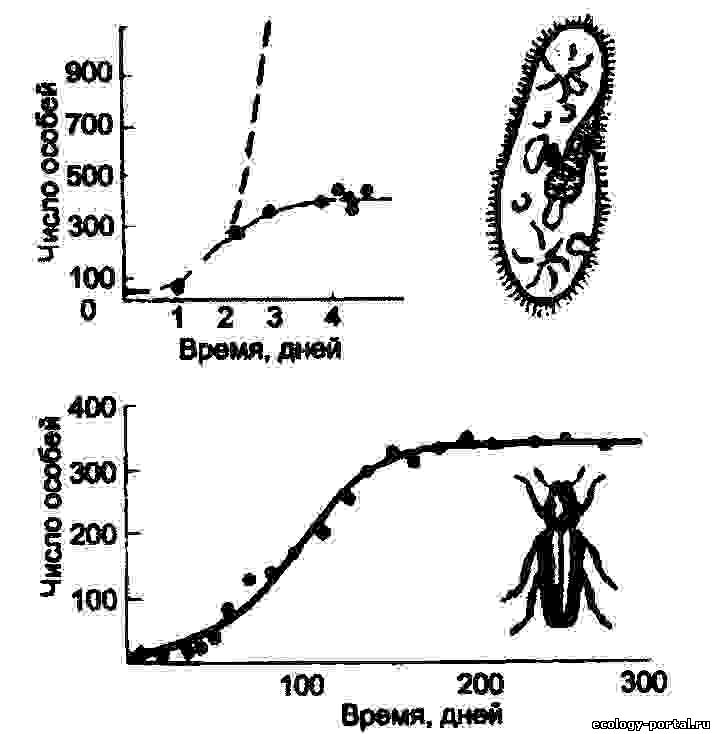
Реальная и теоретическая кривые роста численности инфузорий-туфелек (вверху) и рост численности жуков определенного вида в культуре (численность меняется по правилам логистического роста)
Пунктирная линия — теоретическая кривая (экспонента); сплошная линия — в реальной культуре рост численности замедляется и через определенное время останавливается
В модели экспоненциального роста удельную рождаемость b и удельную смертность d можно обозначить как 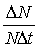 При этом в замкнутой популяции N bNt - dNt;
r = b – d. (9.7)
Если смертность выше рождаемости, то убывание численности тоже описывается уравнением (9.6), но с отрицательным г. Такой процесс называют экспоненциальным затуханием численности.
Модель динамики численности популяции при органиченных ресурсх предложил в 1845 г. французский математик Ферхюльст. Уравнение, которое носит его имя, выглядит так:
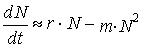 Уравнение Ферхюльста отличается от уравнения экспоненциального роста тем, что в правой его части добавляется выражение mN2. Это выражение учитывает число встреч животных, при которых они могут конкурировать за какой-либо ресурс: вероятность встречи двух особей пропорциональна квадрату численности (точнее, плотности) популяции. У многих животных рост численности популяции действительно ограничивается именно частотой встреч особей. Уравнение Ферхюльста отличается от уравнения экспоненциального роста тем, что в правой его части добавляется выражение mN2. Это выражение учитывает число встреч животных, при которых они могут конкурировать за какой-либо ресурс: вероятность встречи двух особей пропорциональна квадрату численности (точнее, плотности) популяции. У многих животных рост численности популяции действительно ограничивается именно частотой встреч особей.
Перепишем уравнение Ферхюльста следующим образом:
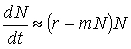 Выражение в скобках — удельная скорость роста численности. Здесь она непостоянна и убывает с увеличением численности популяции. Это отражает усиление конкуренции за ресурсы по мере роста численности. Выражение в скобках — удельная скорость роста численности. Здесь она непостоянна и убывает с увеличением численности популяции. Это отражает усиление конкуренции за ресурсы по мере роста численности.
Если в уравнении (5) вынести в правой части rN за скобки и обозначить за , то получим:
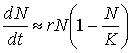 Если N мало по сравнению с k, то выражение в скобках близко к единице: при этом уравнение (9.10) переходит в уравнение экспоненциального роста. График роста численности будет при малых N близок к экспоненте. Когда N близко к k, выражение в скобках близко к нулю, т. е. численность популяции перестает увеличиваться. Отсюда ясно, что k в данной модели — это и есть емкость среды. При N больших, чем k, абсолютный прирост численности становится отрицательным, и численность убывает до величины, равной емкости среды. График зависимости численности популяции от времени, соответствующий решению уравнения (9.10), — S-образная кривая, подобная изображенной на рис. 9.10, внизу. Эта кривая называется логистической кривой, а рост численности, соответствующий уравнению (9.10), —логистический рост. Если N мало по сравнению с k, то выражение в скобках близко к единице: при этом уравнение (9.10) переходит в уравнение экспоненциального роста. График роста численности будет при малых N близок к экспоненте. Когда N близко к k, выражение в скобках близко к нулю, т. е. численность популяции перестает увеличиваться. Отсюда ясно, что k в данной модели — это и есть емкость среды. При N больших, чем k, абсолютный прирост численности становится отрицательным, и численность убывает до величины, равной емкости среды. График зависимости численности популяции от времени, соответствующий решению уравнения (9.10), — S-образная кривая, подобная изображенной на рис. 9.10, внизу. Эта кривая называется логистической кривой, а рост численности, соответствующий уравнению (9.10), —логистический рост.
На логистической кривой роста есть точка, где абсолютная скорость роста численности максимальна. Можно показать, что максимальная скорость роста достигается, когда численность равна.
Популяции, существующие в условиях ограниченных ресурсов, нередко хорошо подчиняются правилам логистического роста.
|





