Генетические процессы в популяциях
Начало генетического изучения популяций положила работа В. Иогансена «О наследовании в популяциях и чистых линиях», опубликованная в 1903 г., где экспериментальным путем была доказана эффективность действия отбора в гетерогенной смеси генотипов (все природные популяции). Была наглядно продемонстрирована неэффективность действия отбора в чистых линиях — генотипически однородном (гомозиготном) потомстве, исходно получаемом от одной самоопыляющейся или самооплодотворяющейся особи.
В настоящее время известно, что все природные популяции гетерогенны и насыщены мутациями. Генетическая гетерогенность любой популяции при отсутствии давления внешних факторов должна быть неизменной, находиться в определенном равновесии. А. В. Яблоков, А. Г. Юсупов (1998) приводят расчеты на двух примерах, впервые сделанные Г. Харди (1908).
Предположим, что в популяции число форм гомозиготных по разным аллелям одного гена (АА и аа) одинаково. Если особи — носители данных аллелей совершенно свободно скрещиваются друг с другом, то возможны следующие комбинации:
Самки
| Самцы
| Самцы
|
| 0,5А
| 0,5А
| 0,5А
0,5а
| 0.25АА
0,25Аа
| 0,25Аа
0,25аа
|
Цифры показывают, что в данном поколении в популяции будут возникать гомозиготы АА и аа с частотой по 0,25, а гетерозиготы Аа — с частотой 0,50. Это же соотношение сохранится и в следующем поколении: частота гамет с рецессивным аллелем а составит 0,5 (0,25 от гомозигот аа+0,25 от гетеро-зигот Аа), также как и частота гамет с доминантным аллелем А (0,25 от гомозигот АА+0,25 от гетерозигот Аа). Это же соотношение сохранится во всех следующих поколениях, если не будет нарушено каким-либо внешним давлением.
Определенно, в подавляющем большинстве случаев в популяции встречается разное число гомозигот АА и аа. Разберем пример, когда частота аллелей данного гена в популяции будет 0,7 а, 0,ЗА:
Самки
| Самцы
| Самцы
|
| q
| (1-q)
| q
(1 - q)
| qq
q (1 - q)
| q(l - q)
(1 - q)(1 - q)
|
При суммировании это дает: 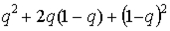 или или 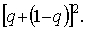
Эта формула носит название формулы Харди—Вайнберга и позволяет рассчитывать относительную частоту генотипов и феноти пов в популяции. Так, предположим, что в популяции каких-либо жуков обнаружены красные формы с частотой 25% (или 0,25) и черные с частотой 75% (или 0,75); черный цвет определяется доминантным аллелем А, а красный — рецессивным аллелем а. При этом частота встречаемости генотипов аа составит (1 —q)2 = 0,2 5, а частота встречаемости аллеля а составит 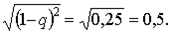 Согласно той же формуле частота доминантного аллеля А составит 1—0,5 = 0,5, а частота гомозиготных доминантных генотипов АА составит в популяции q2 = 0,52 = 0,25. Согласно той же формуле частота доминантного аллеля А составит 1—0,5 = 0,5, а частота гомозиготных доминантных генотипов АА составит в популяции q2 = 0,52 = 0,25.
Итак, при анализе природных совокупностей особей (популяций) необходимо различать понятия: частота гена (количественное соотношение аллелей одного какого-либо локуса), частота генотипа (количественное соотношение разных генотипов) и частота фенотипа (количественное соотношение разных фенотипов).
Формула Харди—Вайнберга пригодна лишь для предельно упрощенной ситуации, для идеальной бесконечно большой популяции (иногда ее называют «менделевской») и при отсутствии давления каких-либо факторов. Кроме того, как известно, на частоту фенотипов оказывает влияние не только частота данного аллеля, но и такие его свойства, как доминантность, рецессивность, пенетрантность и экспрессивность. Таким образом, при анализе природных популяций данная формула применима лишь с большими оговорками.
Существование двух (или более) генетически различных форм в популяции в состоянии длительного равновесия в таких соотношениях, что частоту даже наиболее редкой формы нельзя объяснить только повторными мутациями, называется полиморфизмом. В качестве примера полиморфизма можно привести три формы цветков у примулы (Primula vulgaris),
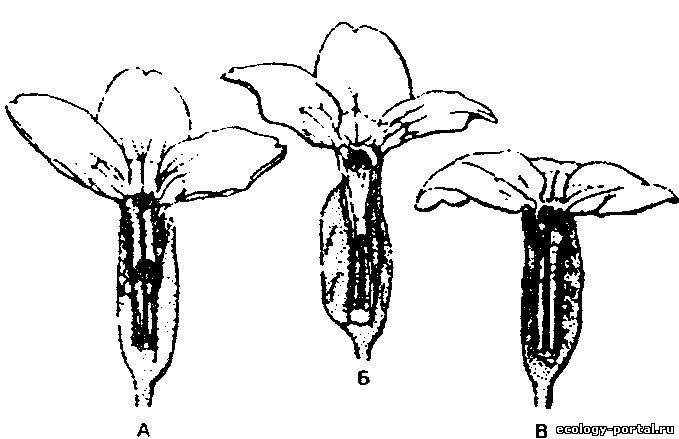
Три формы цветков у примулы (Primula vulgaris),
из Ф. Шеппарда, 1970
В природных популяциях примулы (Primula vulgaris) всегда есть особи с длинным пестиком и короткими пыльниками (А), длинными пыльниками и коротким пестиком (Б) и одинаковыми по длине пыльниками и пестиком (В). Самоопыление возможно только у цветов типа В. Гетеростилия способствует перекрестному оплодотворению.
Полиморфизм по механизму возникновения и поддержания разделяется на две большие группы: гетерозиготный и адаптационный.
Гетерозиготный полиморфизм устанавливается в результате давления на популяцию естественного отбора, положительно отбирающего гетерозигот.
Адаптационный полиморфизм — это две или несколько генетически различных форм внутри популяции, подвергающихся положительному отбору в разных экологических условиях.
В качестве примера можно привести адаптационный полиморфизм в популяции двухточечной тлевой (божьей) коровки Adalia bipunctata
Адаптивный полиморфизм в популяции тлевых
(божьих) коровок Adalia bipunctata:
I — процентное содержание черной и красной форм при весеннем (В) и осеннем (О) сборах; II — частота доминантного гена А (черная окраска) в популяциях весной и осенью каждого года (в%) (по Н. В. Тимофееву-Ресовскому и Ю. М. Свирежеву, 1965)
На протяжении 10 лет в изучении популяции тлевой коровки осенью — при уходе на зимовку — черных форм было от 50 до 70%, а весной — при выходе из зимовки — от 30 до 45%. Красных форм осенью было меньше 50%, а весной — больше. Красные формы, как было установлено, лучше переносят в зимний период холод, а черные — интенсивнее размножаются летом. Отсюда отбор направлен на сохранение большего числа красных жуков зимой и черных — летом. Разнонаправленное давление отбора в отдельные периоды жизни популяции способствует выработке устойчивого адаптационного полиморфизма.
Положение о генетическом единстве популяции является одним из наиболее важных выводов популяционной генетики: любая популяция представляет сложную генетическую систему, находящуюся в динамическом равновесии.
|





